Lisanne Taams, a student at Radboud University in the
Netherlands, is working on a PhD about, in her words, “computing motives of
moduli stacks of vector bundles on stacky curves.”
اضافة اعلان
“It took me two years to even say that properly,” Taams said.
But, she added, such heights of abstraction only elevated her delight as she
recently spent time on a more concrete contemplation: counting the ways that a
square can be divided into similarly proportioned rectangles.
 A photo of 1,371 possible rectangular
proportions that divide a square into seven similar rectangles.
A photo of 1,371 possible rectangular
proportions that divide a square into seven similar rectangles.
She found this geometric puzzle on Mathstodon, a community
within social network Mastodon. Created in the spring of 2017 by two
mathematicians in England, Christian Lawson-Perfect and Colin Wright,
registered accounts on Mathstodon totaled about 3,000 in September. Since then,
with the Twitter exodus, the number has increased to around 13,000.
The puzzle was posted in December by John Carlos Baez, a
mathematical physicist at the University of California, Riverside.
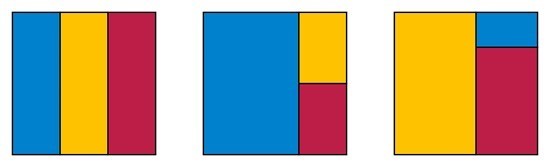
“There are three ways to divide a square into three rectangles
with the same proportions!” Baez wrote.
He illustrated the answer with three images that he borrowed
from Wikipedia.
In one, the rectangles are three times as long as they are wide,
he explained in an email. In the second, the rectangles are 1.5 times as long.
“The third solution is trickier,” Baez said. The rectangles are “about 1.75487
times as long as they are wide, though one rectangle is turned around so it’s
short and squat,” he added.
Baez noted that the number 1.75487 is of interest to
mathematicians. “It’s the square of the ‘plastic ratio,’” he said, “which is a
number that has a lot of properties similar to the more famous ‘golden ratio.’”
 A photo of 245 possible rectangular proportions
that divide a square into six similar rectangles. A puzzle posted in an online community
unlocked a wormhole within the basic shape.
A photo of 245 possible rectangular proportions
that divide a square into six similar rectangles. A puzzle posted in an online community
unlocked a wormhole within the basic shape.
Having laid that foundation, Baez asked his Mathstodon
followers: “What if you chop a square into four similar rectangles? What
proportions can they have?”
Among the first to take the bait was Rahul Narain, a computer
scientist at the Indian Institute of Technology, Delhi. “I was on Mastodon
before it was cool,” he says in his bio (he joined in December 2017). “And the
fact that all the cool people are here now is a bit unsettling.”
Narain sketched out a systematic strategy for solving the puzzle,
though he hoped someone else would carry it out. As he said in his reply to
Baez, “I really have other things I need to work on right now, I can’t afford
to get nerd-sniped any more than this!”
11 solutionsThere turned out to be 11 solutions — 11 ways a square can be
divided into four similarly proportioned rectangles. The solutions gradually
accumulated with crucial input from Ian Henderson, an independent software
developer in the Bay Area, and Daniel Piker in Bristol, England, who works as a
design systems analyst developing software for architects at Foster + Partners.
And a lot of other people also helped, Baez said. “That’s why it
was fun.”
Taams found 11 solutions by hand and soon discovered that she
had made a few mistakes. She then decided to let the computer do the work. She
wrote software and generated some images. But when she checked the progress
online, “I saw other people already had a lot more pictures,” Taams said.
Piker, who enjoys making geometric animations, had drawn all 11
options.
 A photo of three ways to divide a square into
three rectangles with the same proportions.
A photo of three ways to divide a square into
three rectangles with the same proportions.
The simplicity of the problem is what drew him. “I thought it
was kind of cool that there was something so simple that apparently hadn’t been
looked at before,” Piker said.
However, he added, “the maths quickly went beyond my
understanding.”
He could make sense of a proof posted by Taams, though it was
not something that he would have easily produced. She posted an 11-part thread
— with technical passages composed with LaTeX, a scientific typesetting
language — showing that this humble geometry puzzle is connected to more
serious and formal mathematics.
In other words, she came up with a proof that the ratio of the
long sides to the short sides are “algebraic numbers,” a topic that is a major
topic in number theory.
“I don’t think we’ve gotten anywhere near the bottom of this
yet,” Baez said. “But it’s a good step.”
Taams found her proof computationally and then pondered it
further. The computations produced a set of equations, she said. “And then you
wonder, ‘Oh, are these all the equations? Yes or no?’” She convinced herself
the answer was yes by just looking at three examples. “It’s a little bit hard
to argue why,” she said. “If you stare at the pictures, you sort of see it.”
 A photo of 11 ways a square can be
divided into four similarly proportioned rectangles.
A photo of 11 ways a square can be
divided into four similarly proportioned rectangles.
The online discussion at one point turned to a similar
investigation into “squaring the square” by William Tutte and his collaborators
in the 1930s, which is related to electrical circuit theory.
“It turns out you can think of the height and width of each
square as related to voltage and current in an electrical circuit — and using
this, you can find ways to ‘square the square’ using electrical circuit
theory,” Baez said by email. “Something like this is also true for the
rectangle dissection problem, but we haven’t exploited it yet.”
David Eppstein, a computer scientist at the University of
California, Irvine, commented that the term “guillotine partition” is the
standard way to describe the process of recursively slicing off, vertically or
horizontally, rectangular pieces from a square.
Jules Hedges, a computer scientist at the University of
Strathclyde, Glasgow, in Scotland, suggested that “Mondrian” — after Dutch
abstract artist Piet Mondrian — might also be a fitting name for this process.
This prompted Stefano Gogioso, a computer scientist at the University of
Oxford, to point out that, “in machine learning, Mondrian tree/forests is used
to denote a certain kind of classification performed by guillotine cuts.”
Returning to the 11 four-way rectangulations: This result was
confirmed with two batches of code: one by Narain and one by Henderson. They
didn’t stop there.
“The question appeared in my mind, ‘Oh, what about five? What
about six?’” Henderson said. Both he and Narain found 51 solutions to dividing
a square into five similar rectangles.
Henderson found 245 possible rectangular proportions that divide
a square into six similar rectangles and 1,371 options for seven. Initially, he
gave up on eight rectangles; he tried, but the program just kept running.
Eventually, it ran out of memory.
But then he circled back and realized there was something amiss
with the code. “There are (according to the code, at least) 8,506 different
aspect ratios for eight rectangles.” He may try for nine.
Read more Lifestyle
Jordan News





